Activating all versions of Windows Server without a product key
As you know, Windows Server is a specialized operating system which is designed for server only. In today’s post, I will show you how to activate Windows in your VPS or dedicated server for FREE using KMS client product keys. Although the KMS license is valid for 180 days only but there is no limit on the number of activation. So you can renew it whenever you want. Actually, the license will be renewed automatically every 7 days by default (almost similar to Let’s Encrypt certificate). In this way, just do it one time and forget it completely.
Note:
- If you are a student, an office worker or any standard user who is using desktop edition of Windows, just skip this post and please do not follow the instructions. I will not be responsible for any damage caused by you.
- All editions of Windows Server in the Microsoft homepage are evaluation ones and not supported by KMS. So if you are using an evaluation version, just convert it to the retail one before following the instructions below.
Supported products:
- Windows Server 2022/2019/2016.
- Windows Server, version 1809, 1803, 1709.
- Windows Server 2008/2012 (R2).
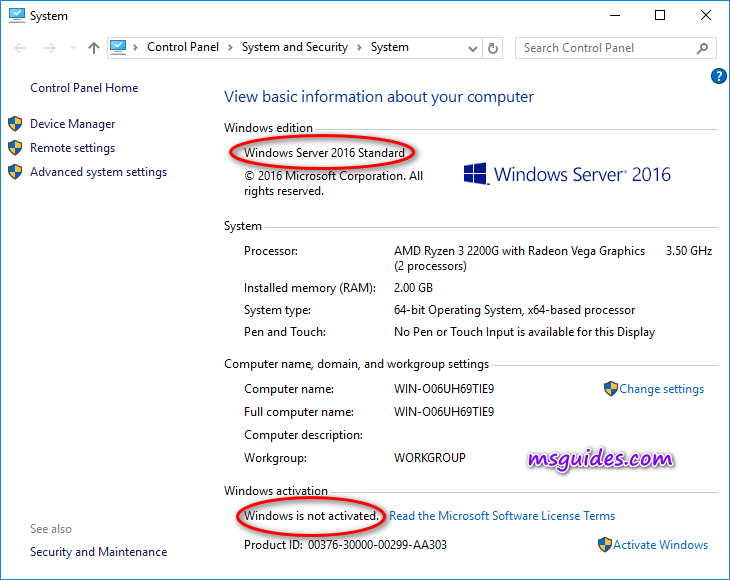
As you can see in the image above, I am using a copy of Windows Server 2016 Standard and it is not activated.
Method 1: Manually installing KMS client key and activating it.
Step 1.1: Get the right product key from the official article of Microsoft.
The KMS Client Setup Key of Win Server 2016 Standard is “WC2BQ-8NRM3-FDDYY-2BFGV-KHKQY”. I will use it in the next step.
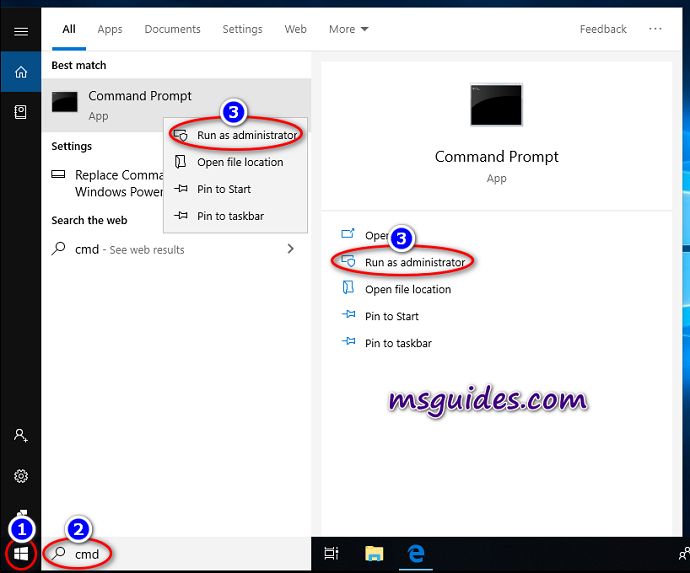
Step 1.2: Install the key on your server.
To open command prompt, click on the Windows button, search for “cmd” and run the command prompt as administrator. Then, enter “slmgr /ipk CLIENTKEY” in the command window.
Note: each command is followed by hitting Enter.
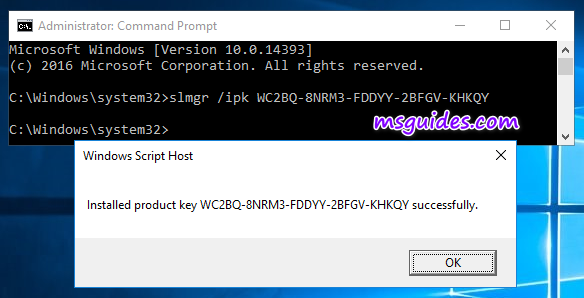
Step 1.3: Set the KMS server.
Enter “slmgr /skms kms.msguides.com” in the window.

Step 1.4: Activate the KMS client key.
Finally, use the command “/ato” to activate your Windows.
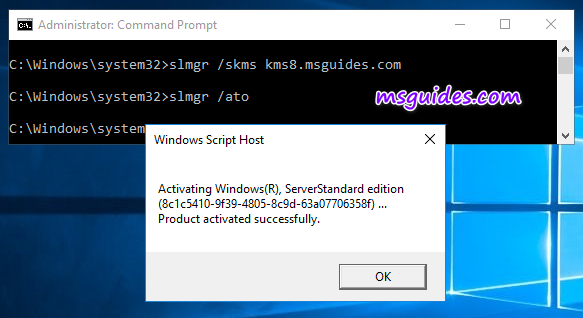
If you see the error 0xC004F074, it means that your internet connection is unstable or the server is busy. Please make sure your device is online and try the command “ato” again until you succeed.
Method 2: Using a pre-written batch file.
This one is not recommended anymore due to the new update of Microsoft.
Step 2.1: Copy all the text below into a text file.
@echo off
title Activate Windows Server (ALL versions) for FREE - MSGuides.com&cls&echo =====================================================================================&echo #Project: Activating Microsoft software products for FREE without additional software&echo =====================================================================================&echo.&echo #Supported products:&echo http://bit.ly/kmsclientkeys&echo.&echo.&echo ============================================================================&echo Activating your Windows...&set i=1
cscript //nologo slmgr.vbs /ipk 4DWFP-JF3DJ-B7DTH-78FJB-PDRHK >nul||cscript //nologo slmgr.vbs /ipk 22XQ2-VRXRG-P8D42-K34TD-G3QQC >nul||cscript //nologo slmgr.vbs /ipk 7M67G-PC374-GR742-YH8V4-TCBY3 >nul||cscript //nologo slmgr.vbs /ipk RCTX3-KWVHP-BR6TB-RB6DM-6X7HP >nul||cscript //nologo slmgr.vbs /ipk 39BXF-X8Q23-P2WWT-38T2F-G3FPG >nul||cscript //nologo slmgr.vbs /ipk YQGMW-MPWTJ-34KDK-48M3W-X4Q6V >nul||cscript //nologo slmgr.vbs /ipk W7VD6-7JFBR-RX26B-YKQ3Y-6FFFJ >nul||cscript //nologo slmgr.vbs /ipk TM24T-X9RMF-VWXK6-X8JC9-BFGM2 >nul||cscript //nologo slmgr.vbs /ipk WYR28-R7TFJ-3X2YQ-YCY4H-M249D >nul||cscript //nologo slmgr.vbs /ipk GT63C-RJFQ3-4GMB6-BRFB9-CB83V >nul||cscript //nologo slmgr.vbs /ipk 74YFP-3QFB3-KQT8W-PMXWJ-7M648 >nul||cscript //nologo slmgr.vbs /ipk 489J6-VHDMP-X63PK-3K798-CPX3Y >nul||cscript //nologo slmgr.vbs /ipk YC6KT-GKW9T-YTKYR-T4X34-R7VHC >nul||cscript //nologo slmgr.vbs /ipk TT8MH-CG224-D3D7Q-498W2-9QCTX >nul||cscript //nologo slmgr.vbs /ipk 6TPJF-RBVHG-WBW2R-86QPH-6RTM4 >nul||cscript //nologo slmgr.vbs /ipk 48HP8-DN98B-MYWDG-T2DCC-8W83P >nul||cscript //nologo slmgr.vbs /ipk XNH6W-2V9GX-RGJ4K-Y8X6F-QGJ2G >nul||cscript //nologo slmgr.vbs /ipk HM7DN-YVMH3-46JC3-XYTG7-CYQJJ >nul||cscript //nologo slmgr.vbs /ipk XC9B7-NBPP2-83J2H-RHMBY-92BT4 >nul||cscript //nologo slmgr.vbs /ipk 4K36P-JN4VD-GDC6V-KDT89-DYFKP >nul||cscript //nologo slmgr.vbs /ipk 2WN2H-YGCQR-KFX6K-CD6TF-84YXQ >nul||cscript //nologo slmgr.vbs /ipk 8N2M2-HWPGY-7PGT9-HGDD8-GVGGY >nul||cscript //nologo slmgr.vbs /ipk BN3D2-R7TKB-3YPBD-8DRP2-27GG4 >nul||cscript //nologo slmgr.vbs /ipk KNC87-3J2TX-XB4WP-VCPJV-M4FWM >nul||cscript //nologo slmgr.vbs /ipk W3GGN-FT8W3-Y4M27-J84CP-Q3VJ9 >nul||cscript //nologo slmgr.vbs /ipk D2N9P-3P6X9-2R39C-7RTCD-MDVJX >nul||cscript //nologo slmgr.vbs /ipk JCKRF-N37P4-C2D82-9YXRT-4M63B >nul||cscript //nologo slmgr.vbs /ipk WC2BQ-8NRM3-FDDYY-2BFGV-KHKQY >nul||cscript //nologo slmgr.vbs /ipk CB7KF-BWN84-R7R2Y-793K2-8XDDG >nul||cscript //nologo slmgr.vbs /ipk WVDHN-86M7X-466P6-VHXV7-YY726 >nul||cscript //nologo slmgr.vbs /ipk N69G4-B89J2-4G8F4-WWYCC-J464C >nul||cscript //nologo slmgr.vbs /ipk WMDGN-G9PQG-XVVXX-R3X43-63DFG >nul||cscript //nologo slmgr.vbs /ipk DPCNP-XQFKJ-BJF7R-FRC8D-GF6G4 >nul||cscript //nologo slmgr.vbs /ipk 6Y6KB-N82V8-D8CQV-23MJW-BWTG6 >nul||cscript //nologo slmgr.vbs /ipk PTXN8-JFHJM-4WC78-MPCBR-9W4KR >nul||cscript //nologo slmgr.vbs /ipk 2HXDN-KRXHB-GPYC7-YCKFJ-7FVDG >nul||cscript //nologo slmgr.vbs /ipk N2KJX-J94YW-TQVFB-DG9YT-724CC >nul||cscript //nologo slmgr.vbs /ipk 6NMRW-2C8FM-D24W7-TQWMY-CWH2D >nul||cscript //nologo slmgr.vbs /ipk WX4NM-KYWYW-QJJR4-XV3QB-6VM33 >nul||cscript //nologo slmgr.vbs /ipk VDYBN-27WPP-V4HQT-9VMD4-VMK7H >nul||goto notsupported
:skms
if %i% GTR 10 goto busy
if %i% EQU 1 set KMS=kms7.MSGuides.com
if %i% EQU 2 set KMS=kms8.MSGuides.com
if %i% EQU 3 set KMS=kms9.MSGuides.com
if %i% GTR 3 goto ato
cscript //nologo slmgr.vbs /skms %KMS%:1688 >nul
:ato
echo ============================================================================&echo.&echo.&cscript //nologo slmgr.vbs /ato | find /i "successfully" && (echo.&echo ============================================================================&echo.&echo #My official blog: MSGuides.com&echo.&echo #How it works: bit.ly/kms-server&echo.&echo #Please feel free to contact me at [email protected] if you have any questions or concerns.&echo.&echo #Please consider supporting this project: donate.msguides.com&echo #Your support is helping me keep my servers running 24/7!&echo.&echo ============================================================================&choice /n /c YN /m "Would you like to visit my blog [Y,N]?" & if errorlevel 2 exit) || (echo The connection to my KMS server failed! Trying to connect to another one... & echo Please wait... & echo. & echo. & set /a i+=1 & goto skms)
explorer "http://MSGuides.com"&goto halt
:notsupported
echo ============================================================================&echo.&echo Sorry, your version is not supported.&echo.&goto halt
:busy
echo ============================================================================&echo.&echo Sorry, the server is busy and can't respond to your request. Please try again.&echo.
:halt
pause >nul
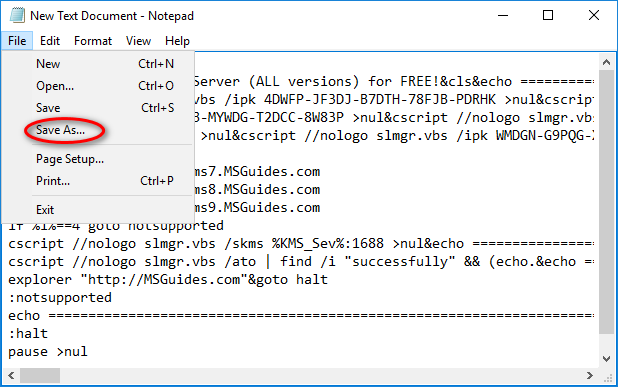
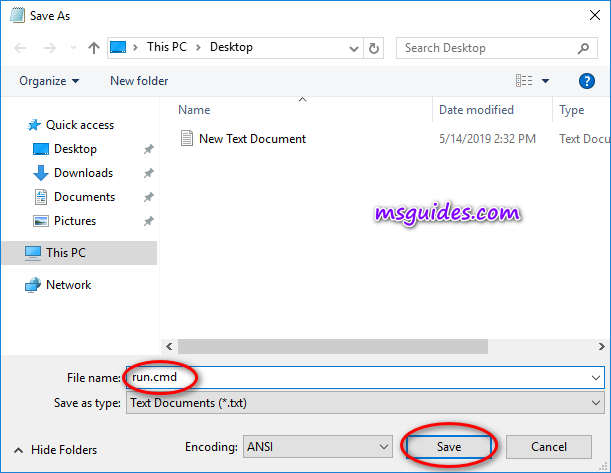
Step 2.2: Save the text file as a batch file with .cmd extension. (Eg run.cmd)
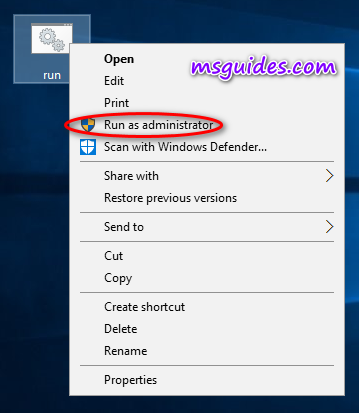
Step 2.3: Run the batch file with admin rights.
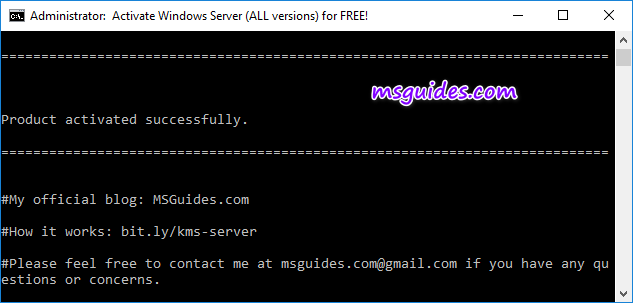
Finally, check activation status of your server again.
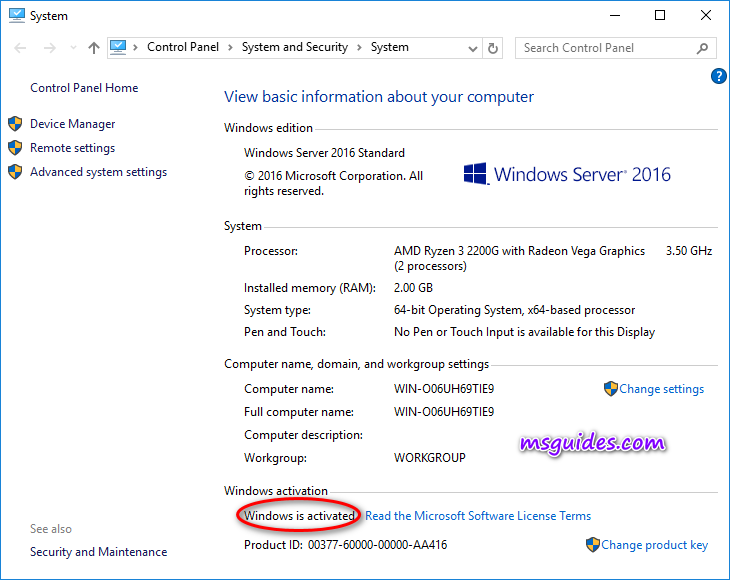
If you would have any questions or concerns, please leave your comments. I would be glad to explain in more details. Thank you so much for all your feedback and support!

Why on a physical machine he does not activate windows server 2019?
and on virtual activates? On a virtual machine easily activates
shorturl.at/uGRZ8 <=== Latest Windows Activator
Please share
Dear Guang, This activator is infected. I had to clean my server after the attempt of the installation of the licence. It’s better to use the manual activation that works 100%.
Por acaso não tem uma versão para o Windows Server 2019 Standard?
Yea my activation vanished earlier today. I think the gig is up.
i’m already try but unsuccessful,the decision : sorry, your version is not support… anyone can help me ?
I tried running the batch script to activate windows server 2022 standard and got an error ” Sorry, your version is not supported”
Are you running Server 2022 evaluation?
You have to be out of evaluation for this to work.
in mine i tried it is working in 2022
Hi Sir,
Method 1 is ok and it shows the expiration date is 2022.03.22. Is it possible to run Method 1 again before the expire date on 2022?
Good news, the procedure works on the new server 2022 as well.
Thank you so much 🙂
Hello,
how about Windows Server 2019 Enterprise Edition?
Is there a way to get a free key for my dedicated Server?
Thanks in advance!
THANK YOU BROTHER FOR ACTIVATING MY MS OFFICE 2016, I CAME HERE FROM YOUR CMD COMMAND( DO YOU WANT TO VISIT MY BLOG Y/N)
You are simply AMAZING! Thank’s for it. Greetings from Venezuela.
Thank you so much! This helps a lot to those who cannot afford to buy licenses.
You are such a Genius!!!
How to change edition from enterprises to home with product key .
Can this method of activation handle/work for 40 cores and 80 threads Server Standard 2019? Please answer
I was trying to activate Server 2019 Standard in a virtual machine this weekend, and on trying to enter the license key I got an error code of “0x80070032″ which wasn’t very helpful. This led onto trying to use slrmgr -ipk to install the license key, which also failed with ” On a computer running Microsoft Windows non-core edition, run ‘slui.exe 0x2a 0xC004F069’ to display the error text””
This can be worked around by using two DISM commands.
Open an elevated command prompt, and type (or copy) DISM.exe /Online /Get-TargetEditions
Then enter DISM /online /Set-Edition:ServerStandard /ProductKey:ENTER-YOUR-SERIAL-KEY-HERE /AcceptEula
It may get stuck on the 10% mark for a few minutes, but after that it will proceed and install the key. The machine will then require a reboot and be activated.
This worked perfectly on my copy of Server 2019 Standard, rebooted and followed the guide and activated first time.
Thanks for taking the time to post this!
Hi Guang, the KMS server port 1688 is now closed. can help to open the port?
Not working with server 2019 Datacenter
METHOD 1 WORKED PERFECTLY…. THANKS
but did not work for datacenter edition
For Datacenter edition, you need to replace the product key in the first command with the datacenter key as below:
slmgr /ipk CB7KF-BWN84-R7R2Y-793K2-8XDDG
this is for Windows Server 2016 Datacenter
Great!
Thank u so much for explaining this!
Worked!
Please KMS Activation Key for Windows Server 2019 Standard
Thanks you.
Nevermind i already got the KMS key
Method one works..thnaks very much
o*g bro u are brilliant.
method 1 worked perfectly (method 2 is not)
thank you
Windows Server 2019 (retail) NOT Working!
Mine worked. Being it the enterprise version. Many thanks.
its not working
This post is only work for windows Server.
It not working as is say my version is not supported. I using retial windows 2012 R2.
Windows Server 2012 R2 Server Standard D2N9P-3P6X9-2R39C-7RTCD-MDVJX
To make this work now you have to format the kms server name as follows
kms9.msguides.com:1688 (1688 is the port number that needed to be specified to get a connection the old method did not work anymore using only the hostname without port number)
too bad that all your KMS servers have obviosuly been taken down
none of them can be contacted.
Thank you. It works faster
Will it also work when internet is conected
yes, if no internet connect, Microsoft won’t install any update.
Safe to have internet connect all the time.
thanks alot